インサイト >

はじめに
以下は、「分散投資」に対するSUSTENの考え方について、厳密性をやや犠牲にしながら、直感的にご理解いただけるよう概説したものです。
分散投資1.0
1940年代以前、リスクを数字で評価するという発想が無かった人々は、目に見えるリターン、つまり「利回り」にばかり着目して投資をしていました。クーポン利回りが3%の債券と配当利回り7%の株式があれば、表面的なリターンが高そうな株式を選択し、利回り3%の債券は魅力に欠けます。もちろん、資金回収が不能になるリスクや事業のリスクを漠然と評価することはありましたが、合�理的な評価手法や理論的考察が発達していた訳ではありません。とにかくリターンを最大化するのが目的である場合、投資行動にリスクの要素が影響を及ぼすことはありませんでした。
平均分散法の登場
投資がギャンブルと大差なかったそのような時代、シカゴ大学の博士課程学生であった若干24才のハリー・マーコウィッツは、当時の投資理論がリスクを全く考慮していないことに疑問を抱きます。そして1952年に自身の理論を論文Portfolio Selectionにて発表しました。その中で提唱した「平均分散法」は現代ポートフォリオ理論のさきがけとなりファイナンス界に歴史を刻みます。そのポイントを要約すると、
- 投資はリターンだけではなく、リスクも同時に評価しなくては意味がない。(リターンとリスクのバランス)
- そのためには、リスクを数値で評価しなくてはいけない。(リスクの定量化)
- その上でリターン、リスク、リスク回避度を総合評価する目的関数を考え、その最適化問題を解くことによってそれぞれの投資対象への配分比率を決めよう。(現代ポートフォリオ理論)
それまで、「一つのかごに卵をもるな」などという、よくわからない言い伝えでひとくくりにされていた「分散投資」。**それが科学になったのです。**たとえ、リターンが低い銘柄であったとしても、組み合わせて活用すれさえすれば全体としてリスクの分散効果が働くため、大きな存在価値があるということが理論的に示されました。
平均分散法によれば、投資対象のリターンやリスク、投資家のリスク回避度がわかっていれば、最適なポートフォリオが�計算できる一方、いくつかの問題点もありました。代表的な問題点としては、各資産がもつ期待リターンの前提値を人間が与えてやる必要があることが挙げられます。リターンの前提値の設定を誤ると、「数式やモデルそのものは正しいのに、なぜか結果が思わしくない」ということが頻繁に起こりました。というのも、リターンの推定は最も困難なタスクの一つであり、いわゆる"garbage-in garbage-out" (モデルに誤った数値を入力することで、誤った解が出力されること)の状態が起きやすい、また投資対象が多くなってくると推定が必要な相関係数の数はその2乗で増えていくため、当時の貧弱な計算機では最適化計算の負荷が高いという課題も深刻でした。
CAPM
そんな中、ウィリアム・シャープが、1964年に資本資産価格モデル、いわゆるCAPMを発表します。
これは、マーコウィッツの平均分散法の最大の課題であった、いかに合理的にリターンを推定するかという課題を克服するため、実務に耐えうるよう改良されたモデルです。
彼の主張は、
証券の期待リターンは、市場ポートフォリオの期待リターンを, 無リスク利子率を、その証券と市場ポートフォリオとの回帰係数(ベータ値)をとしたとき、
\mu_{i} - r_{f} = \beta_i (\mu_{M} - r_{f})
というものです。
無リスク利子率というのは、平たくいうと銀行預金の利子ですから、仮にゼロとしてしまえば、
とまで簡略化できます。
さて、このシンプルな式には3つほど示唆があると思います。
- は共分散行列があればわかるので、単純に市場ポートフォリオの期待リターンさえもとめてしまえば、あらゆるの証券の期待リターンがわかるということ
- リスクの大小を市場ポートフォリオとの共分散(=連動性)と定義すれば 証券のリターンはそのリスクに比例する ということ
- 最適ポートフォリオは、市場ポートフォリオになるということ
特に、最後の3に関しては極めて重要です。つまるところ、
ある条件の下では、最適ポートフォリオは、存在する全ての証券をそれぞれの時価総額の比率で組み合わせたものになる
と言っています。つまり日本株のみで構成する最適ポートフォリオを実現するにはTOPIXを買って終わりということになります。逆に言えば、時価総額の比率を無視するすべての銘柄選択は、最適では無いということになります。
なんとリターンの予測などしなくても、最適なポートフォリオはすでにわかっていたのです。苦労して最適化計算をする必要などそもそもなかったどころか、最適なポートフォリオを構築するという観点においては証券リターンに対して独自の見通しを持つこと自体が誤りになるというのです。
投資家が把握する必要があるのは、変動リスクに対するリスク許容度のみであり、リスク許容度さえ分かってしまえば投資家にとって最適なポートフォリオは複雑な計算をせずともすぐに決定されます。
これがSUSTENでいうところの「分散投資1.0」の考え方であり、一般的なロボットアドバイザー含め、現在「分散投資」とされているものの多くはこの理論に基づいています。
分散投資1.0に対する疑問
さて1964年に発表されたCAPMは、学術界で大注目を浴びる一方、それまでの常識を覆す結論であったため、学者の間で大きな論争を巻き起こします。
CAPMに対するもっとも多かった反論の一つは、「期待リターンをベータ(市場ポートフォリオとの連動性)だけで説明できるわけなどない。」というものです。たしかに、経済成長率の鈍化、インフレーション、地政学的リスク、流動性枯渇、自然災害など、上げればキリがない様々な種類のリスクを��ひとくくりにして、ベータ値一つで説明しようとするものですから、その反応も不自然ではありません。(実際にその反論を出発点として、Fama Frenchの3ファクターモデルやStephen Rossの裁定価格理論(APT)などへと後に拡張されることになります。)
また、CAPMの問題は導出そのもの(つまり式の展開)自体にはそれほど問題は無いのですが、その理論が成立するための前提条件が実際のマーケットと掛けはなれており現実的ではないという指摘もよくなされます。この前提条件は、物理学でいうところの「真空状態を仮定すると、・・」や「摩擦がないものとしたとき、・・」などという条件と同様に、複雑な世界を美しくモデル化する際には大いに役立ちますが、様々な制約条件が重なり合う現実世界ではそのまま適用することができません。そして、前提が異なると、結論も異なります。
実際にどのような前提条件があるかというと、
- 証券が無限小単位で取引可能であること
- 市場は効率的であり、取引にかかるコストや税金も発生しない
- すべての投資家が市場に対して同一の見通しをもっていて、平均分散法により最適化している
- すべての投資家が無リスク利子率で無限に借り入れを行える
- すべての証券は空売りが可能
などです。
しかし御存知の通り、一部の例外を除いて税金からは逃れられませんし、市場参加者は独自のデータや理論を駆使し、市場コンセンサスを疑い日々知恵を絞っています。すっかりデジタル社会になった現代でも、情報が完全に市場に織り込まれるには一定の時間を要しますし、ほとんどの機関��投資家は借り入れを行って株式を購入することはそもそも認められてすらいません。理論が求める仮定は、残念ながら現実世界ではあてはまらないのです。
一部の論者には、「仮にすべての市場参加者がこの前提に当てはまらなくとも、一部の市場参加者が市場の非効率性を解消する」という主張が見られますが、私たちの知る限り市場の非効率性をなくせるほど無限に借り入れを行い、市場に流動性を提供でき、かつ取引コストを無視できるような主体は存在しません。
ゼロ・ベータ戦略
さて、理論の世界と現実世界の”ズレ”を実感するには、どうすればよいでしょうか。最も直感的な方法の一つは、「ベータ値が0で期待リターンが正であるような資産や投資戦略を構築してみること」です。分散投資1.0の世界では、ベータ値がゼロの戦略には期待リターンが存在しないことになっていますので、このような方法で長期的にリターンが得られる戦略が見つかると、分散投資1.0の世界は現実世界には当てはまらないことが示されます。
例えば、マクロ経済や市場のデータを参考に、ある資産を買い、同時にまた別の資産を売るという戦略を考えてみます。(これはロング・ショート戦略と呼ばれます)
通常、ある資産を買う(=ロング)とその資産固有の収益源が得られるという利点があるものの、市場全体との連動性が生じます。市場との連動性が生まれるということはすなわち、たとえその資産固有の収益源がプラスであっても、景気後退局面で市場全体が大幅に下落してしまうと、結局マイナスがでてしまうということも少なくありません。そこで、その�余計なリスクを、別の資産を売る(=ショート)ことで市場に対する連動性を低減して(ヘッジして)しまおうという考え方です。
より具体例をもって示すと、例えば、2020年末時点でドイツの10年国債が魅力的であったため、投資を決定したとしましょう。2021年に入り、ドイツの10年債そのものの魅力に変化はありませんでしたが、残念ながらグローバルの金利上昇のあおりを受けて2月末までに債券価格は2.5%以上下落しました。昨年末から100万円相当のドイツ10年国債を買い持ちしていると2万5千円失う計算になります。
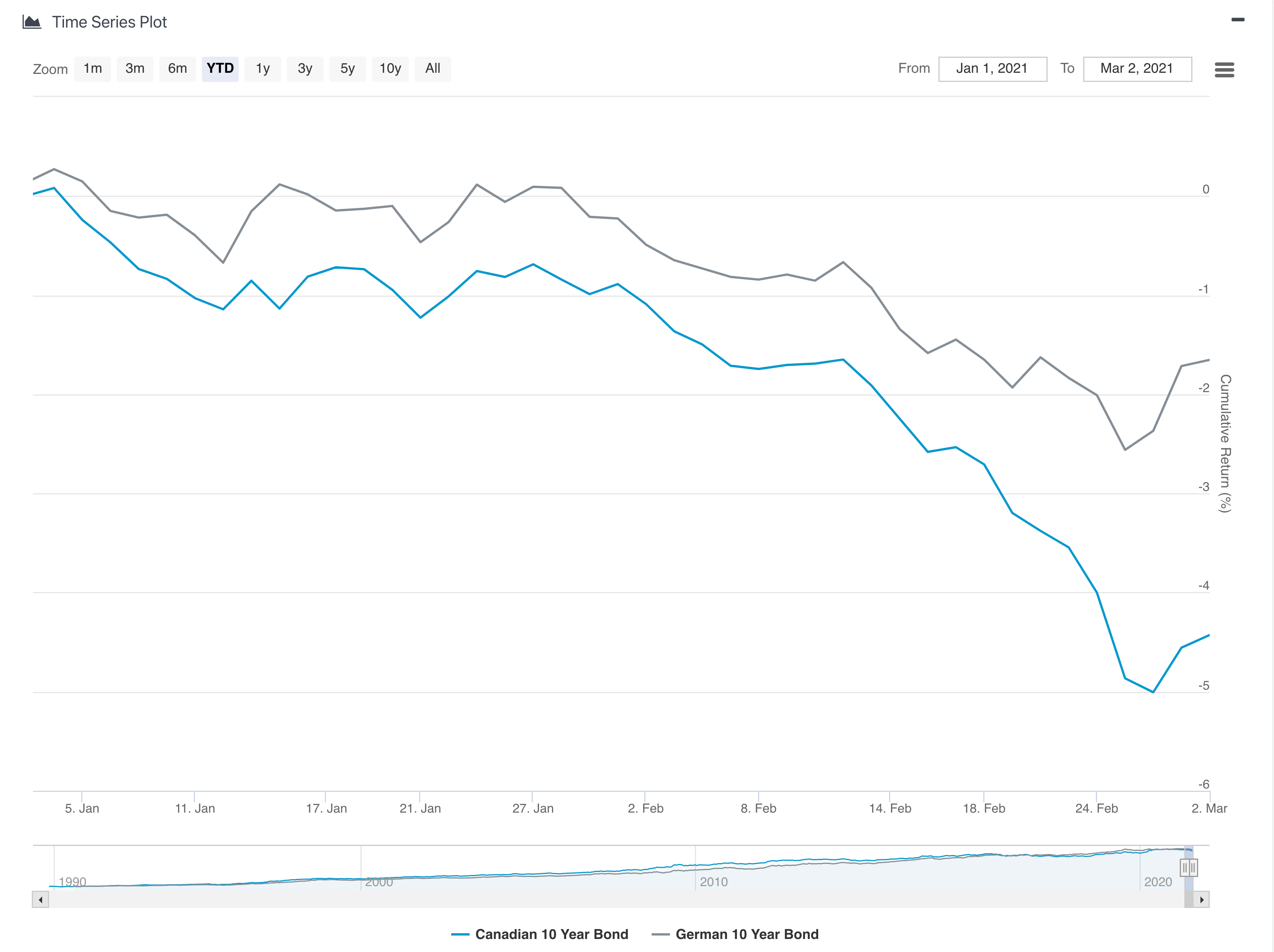
そこで、同時に魅力度の低い投資対象であったカナダ10年国債の売建をしていたらどうなっていたでしょうか。カナダの10年国債価格は同時期に5%下がっていますので、2月末には95万相当まで価値が低下しており、そこで買い戻しを行うと差し引き5万円のプラスになります。
両者をまとめると、合計でプラス2.5万円(=ドイツの買いから2.5万円の損失、カナダの売りから5万円の利益)となり、世界的な債券価格の下落傾向にも関わらず、収益を確保できたことになります。ここで、債券市場全体が上昇したとしても、ドイツがカナダを上回って上昇してさえすれば依然として収益はプラスになることに注意してください。**つまり、「両者の価格差」が問題なのであって市場が上がるか下がるかの方向性はもとより関係ありません。**市場の連動性はこのロングショート戦略に大きな影響を与えず、「ドイツとカナダの相対的魅力�度」がこの戦略の可否に直接的な影響を与えるのです。
さて、いったん何を根拠にドイツとカナダの相対的魅力度を判断したかはさておき、この「市場との連動性がない戦略でリターンが得られた」ことは、分散投資1.0の考え方に一石を投じます。
CAPMの主張は「無リスク金利を上回るリターンは、ベータ(市場との連動性)から生まれるのであり、それ以外に存在しない。」というものなので、もしもCAPMが正しいならば、プラスの期待リターンを得る唯一の方法は市場連動性を受け入れる(=ベータをとる)こと以外にありえません。すなわちベータがゼロであれば、リターンの期待値はゼロであるため、短期的に上振れ・下振れはすれど、長期的に累積収益率はゼロに収斂していくはずなので上記と矛盾しています。
つまり考えうるのは以下の2パターンのどちらかです。
- CAPMは正しい。ゼロ・ベータでありながら期待リターンがプラスになるものは存在するはずがないで、リターンがプラスになったのは単なる偶然である。
- CAPMでは説明が及ばない部分がある。市場ベータ以外からの収益源が少なからず存在する。
さまざまなバリエーションがあるものの、以上が60年代以降続けられてきたCAPM論争の黄金パターンです。生み出されたリターンが偶然の産物であるという帰無仮説を立てて検定を行い棄却していくという作業を地道に行うことになります。
SUSTENの考え方:分散投資2.0
SUSTENも例にもれず、上記2の立場をとっています。たしかに市場は伝統的な理論が主張する通り、相当効率的であると言え、特に市場の短期的な上下動の�予測は極めて難しいと言わざるを得ません。しかし、一方で完全に効率的ではないのも確かです。そこで、SUSTENでは伝統的ポートフォリオ理論を補正して、分散投資のフレームワークを独自に構築しています。
たとえば、上記のドイツ国債/カナダ国債の例は、説明目的で単純化してはいるものの、実際に当社の自動運用アルゴリズムがトレードしたポジションの一部です。全体ではグローバル各国の株式市場、債券市場、通貨市場を監視し、国別の株式・債券・通貨の投資妙味、および資産クラス間の魅力度(株式vs債券vs通貨)を合わせて投資対象の選定と投資額の決定をおこない世界中の証券取引所において日々取引を執行しています。
また以下に、**グローバル複合戦略ポートフォリオ(G)**において、アルゴリズムが投資妙味を判断する際に評価軸としているものをご紹介します。グローバル資産分散ポートフォリオ(R)/**グローバル債券ポートフォリオ(B)**が世界経済全体の成長を獲得しているのと対照的に、古典的理論では存在しないことになっている収益源(=リスク・プレミアム)の長期的な獲得を目指しています。
| 分類 | 概要/背景 | 関連する認知バイアス | 得意な環境 | 苦手な環境 |
|---|---|---|---|---|
| モメンタム | 情報伝達の遅延に由来する価格変動の趨勢 | バンドワゴン効果 ハウスマネー効果 | 持続的な上昇 または下落 | 一定のレンジ内の動き トレンドの転換期 |
| バリュー | 本源的価値に対して割安な資産への投資 | 外挿効果 損失回避バイアス | 景気サイクルの回復期 | 景気サイクルの上昇後期 |
| キャリー | インカム・ゲインと収益率の連動性 | フォワード・プレミアム・バイアス | 穏やかな金融緩和局面 | 流動性枯渇局面 |
| ディフェンシブ | 高リスク資産への過大評価 | レバレッジ回避効果 | 株式と債券の 逆相関局面 | 株式と債券の 同時下落局面 |
| スキュー | 収益率分布の非線形性に付随するリスク・プレミアム | 宝くじ効果 | 標準的な上下動が 続く局面 | 市場急落または 急上昇局面 |
| フロー | 市場参加者の投資行動パターン | 回帰の誤謬 | 平均からの乖離が 縮小する局面 | 平均からの乖離が 拡大する局面 |
上記のいずれも、リスク・プレミアムという名が示す通り短期的な下落リスクを抱えることにより長期的に対価を得るものです。そ��の意味では伝統的な株式投資と全く同じ原理です。株式市場が景気サイクルや経済の好況不況に左右されながら上昇していくのと同様に、**全てのリスク・プレミアムは環境によって機能しやすい時期としづらい時期があります。**一つの収益源泉が常にプラスのリターンを出し続けるものではないからこそ、特色の異なる複数の収益源にあらかじめ分散しておくことが肝要であると言えます。
